Exchange Entrypoint (spin 16)
This section is referring to wiki page-18 of gist section-14 that is inherited from the gist section-101 by prime spin-27 and span- with the partitions as below.
/maps
Spinors vs Antispinor
One consequence of this is that, in 4 dimensions, we cannot talk about rotation about a line the only non-trivial rotation fixes a plane.
Thus, these cubic monomials with one free vector index have 32 × 11 − 32 = 320 degrees of freedom and are in the {320} representation.
In physics, and specifically in quantum field theory, a bispinor is a mathematical construction that is used to describe some of the fundamental particles of nature, including quarks and electrons.
- It is a specific embodiment of a spinor, specifically constructed so that it is consistent with the requirements of special relativity.
- Bispinors transform in a certain “spinorial” fashion under the action of the Lorentz group, which describes the symmetries of Minkowski spacetime.
- They occur in the relativistic spin-1/2 wave function solutions to the Dirac equation.
- Bispinors are so called because they are constructed out of two simpler component spinors, the Weyl spinors.
- Each of the two component spinors transform differently under the two distinct complex-conjugate spin-1/2 representations of the Lorentz group.
- This pairing is of fundamental importance, as it allows the represented particle to have a mass, carry a charge, and represent the flow of charge as a current, and perhaps most importantly, to carry angular momentum.
- More precisely, the mass is a Casimir invariant of the Lorentz group (an eigenstate of the energy), while the vector combination carries momentum and current, being covariant under the action of the Lorentz group.
- The angular momentum is carried by the Poynting vector, suitably constructed for the spin field.[1]
- A bispinor is more or less “the same thing” as a Dirac spinor. The convention used here is that the article on the Dirac spinor presents plane-wave solutions to the Dirac equation using the Dirac convention for the gamma matrices. That is, the Dirac spinor is a bispinor in the Dirac convention.
By contrast, the article below concentrates primarily on the Weyl, or chiral representation, is less focused on the Dirac equation, and more focused on the geometric structure, including the geometry of the Lorentz group. Thus, much of what is said below can be applied to the Majorana equation. (Wikipedia)
Matter vs Antimatter
Giving a specific example of a result obtained with data from the ATLAS experiment, Priscilla Pani, ATLAS experiment co-convener of the LHC Dark Matter Working Group, highlights how the collaboration has recently searched the full LHC dataset from the machine’s second run (Run 2), collected between 2015 and 2018, *to look for instances in which the Higgs boson might decay into dark-matter particles. “We found no instances of this decay but we were able to set the strongest limits to date on the likelihood that it occurs,”” says Pani. (CERN)
In order to be four-spinors like the electron and other lepton components, there must be one quark component for every combination of flavour and colour, bringing the total to 24 (3 for charged leptons, 3 for neutrinos, and 2·3·3 = 18 for quarks). Each of these is a four component bispinor, for a total of 96 complex-valued components for the fermion field. (Wikipedia)
24 x π(7) = 32 x π(π(11)) = 96
$True Prime Pairs:
(5,7), (11,13), (17,19)
layer | node | sub | i | f. MEC 30 / 2
------+------+-----+-----+------ ‹--------------------------- 30 {+1/2}
| | | 1 | --------------------------
| | 1 +-----+ |
| 1 | | 2 | (5) |
| |-----+-----+ |
| | | 3 | |
1 +------+ 2 +-----+---- |
| | | 4 | |
| +-----+-----+ |
| 2 | | 5 | (7) |
| | 3 +-----+ |
| | | 6 | 11s ‹-- ∆28 = (71-43)
------+------+-----+-----+------ } (36) |
| | | 7 | |
| | 4 +-----+ |
| 3 | | 8 | (11) |
| +-----+-----+ |
| | | 9 | ‹-- ∆18 = (89-71) |
2 +------| 5* +-----+----- |
| | | 10 | |
| |-----+-----+ |
| 4 | | 11 | (13) --------------------- ∆32 ✔️
| | 6 +-----+ ‹------------------------------ 15 {0}
| | | 12 |---------------------------
------+------+-----+-----+------------ |
| | | 13 | |
| | 7 +-----+ |
| 5 | | 14 | (17) |
| |-----+-----+ |
| | | 15 | 7s ‹-- ∆24 = (43-19)
3* +------+ 8 +-----+----- } (36) |
| | | 16 | |
| |-----+-----+ |
| 6 | | 17 | (19) |
| | 9 +-----+ |
| | | 18 | -------------------------- ∆68 ✔️
------|------|-----+-----+----- ‹------ 0 {-1/2}
$True Prime Pairs:
(5,7), (11,13), (17,19)
| 169-1🌀 | 329+289 | ✔️
-----+-----+-----+-----+-----+ ----------------------------------> 1st-gap
1' | 1 | {2} | 3 | 4 | 4¤
+-----+-----+-----+-----+ ---------> 2nd-gap inside the 1st-gap
2' | 5 | 6 | 7 | 8 | 4¤
+-----+-----+-----+-----+ ---------> 2nd-gap inside the 1st-gap
3' | 9 |{10} | 2¤ (M dan F)
+-----+-----+-----+ ---------------> 2nd-gap inside the 1st-gap
4' | 11 | 12 | 13 | 3¤
+-----+-----+-----+-----+ ---------> 2nd-gap inside the 1st-gap
5' | 14 | 15 | 16 | 17 | 4¤
+-----+-----+-----+-----+ ---------> 2nd-gap inside the 1st-gap
6' | 18 | 19 |{20} | 3¤
-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ----> 2nd-gap
∑ | 21 | 22 | 23 | 24 |{25} | 26 | 27 | 28 | 29 | 9¤
-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ----> 1st-gap
∆ ∆ ∆ ∆ ∆ ∆ ∆ ∆ 👆
| | | | | | | | P(7)=142857
8 x 3rd-gap inside the 2nd-gap (Truncated)
Rate to Infinity
This is because spinors need 32 components in 11 dimensions. 11D supergravity can be compactified down to 4 dimensions which then has OSp(8\4) symmetry. (We still have 8 × 4 = 32 so there are still the same number of components.) Spinors need 4 components in 4 dimensions. This gives O(8) for the gauge group which is too small to contain the Standard Model gauge group U(1) × SU(2) × SU(3) which would need at least O(10). (Wikipedia)
32 = 8 x 4 = 2³ x 2² = 2⁵
Eigenvalue curves (right) showing a triple eigenvalue at zero for τ = 1 and double eigenvalues at 1 ± √2i for τ = 4/√3. On the left the graph of 1/Q(λ) with the same eigenvalue curves plotted in the ground plane. Green stars indicate the eigenvalues of A, blue stars the roots of puv(λ) and triangles the zeroes of Q(λ) (Global properties of eigenvalues - pdf)
Digital Root (32) = triple (3) + double (2) = 5 eigenvalues
100 + 68 + 32 = 168 + 32 = π(1000) + 32 = 200
The plot shows the eigenvalues of A + tuu > J for 0 ≤ t ≤ 125000 in red, and the eigenvalues of A − tuu>J for the same range of t in cyan
- Then, one checks easily that A is J-Hamiltonian, and that u >JAu = 0, while u >JA3u = −4 6= 0.
- The polynomial puv(λ) for v = −Ju is constant, equal to −4.
- Hence all the four eigenvalues † of A + tuu >J **are going to infinity””, as is shown in thefollowing figure.
Note also that the rate of convergence to infinity in this example should be as the fourth root of t, which is confirmed by the graph (the fourth root of 125000 is about 19). (Global properties of eigenvalues)
4 x 8 = 32 = 2⁵
The Prime Recycling ζ(s):
(2,3), (29,89), (36,68), (72,42), (100,50), (2,3), (29,89), ...**infinity**
----------------------+-----+-----+-----+ ---
7 --------- 1,2:1| 1 | 30 | 40 | 71 (2,3) ‹-------------@---- |
| +-----+-----+-----+-----+ | |
| 8 ‹------ 3:2| 1 | 30 | 40 | 90 | 161 (7) ‹--- | 5¨
| | +-----+-----+-----+-----+ | | |
| | 6 ‹-- 4,6:3| 1 | 30 | 200 | 231 (10,11,12) ‹--|--- | |
| | | +-----+-----+-----+-----+ | | | ---
--|--|-----» 7:4| 1 | 30 | 40 | 200 | 271 (13) --› | {5®} ✔️ |
| | +-----+-----+-----+-----+ | | |
--|---› 8,9:5| 1 | 30 | 200 | 231 (14,15) ---------› | 7¨
289 | +-----+-----+-----+-----+-----+ | |
| ----› 10:6| 20 | 5 | 10 | 70 | 90 | 195 (19) --› Φ | {6®} ✔️
--------------------+-----+-----+-----+-----+-----+ | ---
67 --------› 11:7| 5 | 9 | 14 (20) --------› ¤ | |
| +-----+-----+-----+ | |
| 78 ‹----- 12:8| 9 | 60 | 40 | 109 (26) «------------ | 11¨
| | +-----+-----+-----+ | | |
| | 86‹--- 13:9| 9 | 60 | 69 (27) «-- 2×Δ9 (2×MEC30) | {2®} ✔️ |
| | | +-----+-----+-----+ | | ---
| | ---› 14:10| 9 | 60 | 40 | 109 (28) ------------- | |
| | +-----+-----+-----+ | |
| ---› 15,18:11| 1 | 30 | 40 | 71 (29,30,31,32) ---------- 13¨
329 | +-----+-----+-----+ |
| ‹--------- 19:12| 10 | 60 | {70} (36) ‹--------------------- Φ |
-------------------+-----+-----+ ---
786 ‹------- 20:13| 90 | 90 (38) ‹-------------- ¤ |
| +-----+-----+ |
| 618 ‹- 21,22:14| 8 | 40 | 48 (40,41) ‹---------------------- 17¨
| | +-----+-----+-----+-----+-----+ | |
| | 594 ‹- 23:15| 8 | 40 | 70 | 60 | 100 | 278 (42) «-- |{6'®} ✔️
| | | +-----+-----+-----+-----+-----+ | | ---
--|--|-»24,27:16| 8 | 40 | 48 (43,44,45,46) ------------|---- |
| | +-----+-----+ | |
--|---› 28:17| 100 | {100} (50) ------------------------» 19¨
168 | +-----+ |
| 102 -› 29:18| 50 | 50(68) --> 3×∆9-∆9=Δ18 goes to unknown |
----------------------+-----+ ---
Elementary Structure
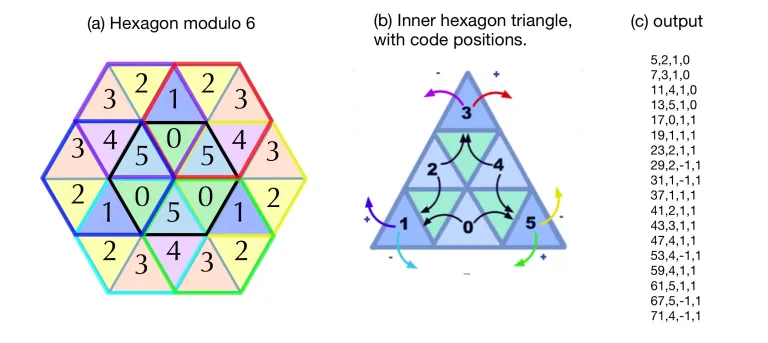
You may refer to the structure of minor hexagon it shows that this reversal behaviour is linked to the nature of the prime numbers.
Aside from 2 and 3, primes come in two flavors, 1 modulo 6 and 5 modulo 6, or the dark and light blue triangles in figure 2(a). The program determines where primes land in the hexagon by moving between the 6 possible positions where primes may land, figure 2(b) . The 1-type primes land in python cells 1, 3, and 5. The 5-type primes land in 0, 2, and 4 cells. Finally, it can print output in the form of figure 2(c). (HexSpin)
Here we are using the inverse function to exponentiation by 3 x 6 = 18 spins. This is what we mean by the multiplication zones that is applied to each of addition zones.
The three (3) minor hexagons are surrounded by the primes (19, 43, 71) which is close to the multiplication of six (6) with 3, 7, 12 to 18, 42, 72. One of a mysterious thing is that 19 × 6 = 43 + 71 where ∆1 is balancing and keep them to remain stay on the 18s scheme. Therefore we use the primes 43 and 71 as corresponding eigenvalues which is the factor by which the eigenvector is scaled.
19 x 6 = 43 + 71 = 114

f(30) = 66 - 30 - 30 - 5 = 1
p r i m e s
1 0 0 0 0 0
2 1 0 0 0 1 ◄--- #29 ◄--- #61 👈 1st spin
3 2 0 1 0 2 👉 2
4 3 1 1 0 3 👉 89 - 29 = 61 - 1 = 60
5 5 2 1 0 5 👉 11 + 29 = 37 + 3 = 40
6 👉 11s Composite Partition ◄--- 102 👈 4th spin
6 7 3 1 0 7 ◄--- #23 👈 1 ◄--- break MEC30 symmetry ✔️
7 11 4 1 0 11 ◄--- #19 ◄--- #43 ◄--- 24s 👈 30
8 13 5 1 0 13 ◄--- #17 ◄--- #49 ◄--- 32s 👈 30
9 17 0 1 1 17 ◄--- 7th prime 👈 5 ◄--- antisymmetric state ✔️
18 👉 7s Composite Partition ◄--- 168 👈 7th spin
10 19 1 1 1 ∆1 ◄--- 0th ∆prime ◄--- Fibonacci Index #18
-----
11 23 2 1 1 ∆2 ◄--- 1st ∆prime ◄--- Fibonacci Index #19 ◄--- #43
..
..
40 163 5 1 0 ∆31 ◄- 11th ∆prime ◄-- Fibonacci Index #29 👉 11
-----
41 167 0 1 1 ∆0
42 173 0 -1 1 ∆1
43 179 0 1 1 ∆2 ◄--- ∆∆1
44 181 1 1 1 ∆3 ◄--- ∆∆2 ◄--- 1st ∆∆prime ◄--- Fibonacci Index #30
..
..
100 521 0 -1 2 ∆59 ◄--- ∆∆17 ◄--- 7th ∆∆prime ◄--- Fibonacci Index #36 👉 7s
-----
These features are the solution to arrange 30 files located in in four (4) of zone folders as the lexer to cope with the Prime Spin and MEC30 Structure.
Now such interaction between the elementary particles can be described by means of a field of force, just as the interaction between the charged particles is described by the electromagnetic field. The above considerations show that the interaction of heavy particles with this field is much larger than that of light particles with it.
- Now the binding energy of the proton in C12, which is estimated from the difference of masses of C12 and B11, is. This corresponds to a binding energy 0,0152 in mass unit, being thirty (30) times the electron mass. (page 53)
- Assuming λ=5×10-¹²cm, we.obtain for me a value 2×10² times as large as the electron mass. As such a quantum with large mass and positive or negative charge has never been found by the experiment, the above theory seems to be on a wrong line. We can show, however, that, in the ordinary nuclear transformation, such a quantum can not be emitted into outer space. (page 54)
The interaction of such a quantum with the heavy particle should be far greater than that with the light particle in order to account for the large interaction of the neutron and the proton as well as the small probability of β-disintegration. (Yukawa - pdf)
The Prime Recycling ζ(s):
(2,3), (29,89), (36,68), (72,42), (100,50), (2,3), (29,89), ...**infinity**
----------------------+-----+-----+-----+ ---
7 --------- 1,2:1| 1 | 30 | 40 | 71 (2,3) ‹-------------@---- |
| +-----+-----+-----+-----+ | |
| 8 ‹------ 3:2| 1 | 30 | 40 | 90 | 161 (7) ‹--- | 5¨
| | +-----+-----+-----+-----+ | | |
| | 6 ‹-- 4,6:3| 1 | 30 | 200 | 231 (10,11,12) ‹--|--- ✔️ | |
| | | +-----+-----+-----+-----+ | | | ---
--|--|-----» 7:4| 1 | 30 | 40 | 200 | 271 (13) --› | {5®} | |
| | +-----+-----+-----+-----+ | | |
--|---› 8,9:5| 1 | 30 | 200 | 231 (14,15) ---------› ✔️ | 7¨
289 | +-----+-----+-----+-----+-----+ | |
| ----› 10:6| 20 | 5 | 10 | 70 | 90 | 195 (19) --› Φ | {6®} |
--------------------+-----+-----+-----+-----+-----+ | ---
67 --------› 11:7| 5 | 9 | 14 (20) --------› ¤ | |
| +-----+-----+-----+ | |
| 78 ‹----- 12:8| 9 | 60 | 40 | 109 (26) «------------ | 11¨
| | +-----+-----+-----+ | | |
| | 86‹--- 13:9| 9 | 60 | 69 (27) «-- 2×Δ9 (2×MEC30) | {2®} | |
| | | +-----+-----+-----+ | | ---
| | ---› 14:10| 9 | 60 | 40 | 109 (28) ------------- | |
| | +-----+-----+-----+ | |
| ---› 15,18:11| 1 | 30 | 40 | 71 (29,30,31,32) ---------- 13¨
329 | +-----+-----+-----+ |
| ‹--------- 19:12| 10 | 60 | {70} (36) ‹--------------------- Φ |
-------------------+-----+-----+ ---
786 ‹------- 20:13| 90 | 90 (38) ‹-------------- ¤ |
| +-----+-----+ |
| 618 ‹- 21,22:14| 8 | 40 | 48 (40,41) ‹---------------------- 17¨
| | +-----+-----+-----+-----+-----+ | |
| | 594 ‹- 23:15| 8 | 40 | 70 | 60 | 100 | 278 (42) «-- |{6'®} |
| | | +-----+-----+-----+-----+-----+ | | ---
--|--|-»24,27:16| 8 | 40 | 48 (43,44,45,46) ------------|---- |
| | +-----+-----+ | |
--|---› 28:17| 100 | {100} (50) ------------------------» 19¨
168 | +-----+ |
| 102 -› 29:18| 50 | 50(68) --> 3×∆9-∆9=Δ18 goes to unknown |
----------------------+-----+ ---
Speaking of the Fibonacci number sequence, there is symmetry mirroring the above in the relationship between the terminating digits of Fibonacci numbers and their index numbers equating to members of the array populating the Prime Spiral Sieve.

The Prime Recycling ζ(s):
(2,3), (29,89), (36,68), (72,42), (100,50), (2,3), (29,89), ...**infinity**
----------------------+-----+-----+-----+ ---
7 --------- 1,2:1| 1 | 30 | 40 | 71 (2,3) ‹-------------@---- |
| +-----+-----+-----+-----+ | |
| 8 ‹------ 3:2| 1 | 30 | 40 | 90 | 161 (7) ‹--- | 5¨
| | +-----+-----+-----+-----+ | | |
| | 6 ‹-- 4,6:3| 1 | 30 | 200 | 231 (10,11,12) ‹--|--- | |
| | | +-----+-----+-----+-----+ | | | ---
--|--|-----» 7:4| 1 | 30 | 40 | 200 | 271 (13) --› | {5®} | |
| | +-----+-----+-----+-----+ | | |
--|---› 8,9:5| 1 | 30 | 200 | 231 (14,15) ---------› | 7¨
289 | +-----+-----+-----+-----+-----+ | |
| ----› 10:6| 20 | 5 | 10 | 70 | 90 | 195 (19) --› Φ | {6®} |
--------------------+-----+-----+-----+-----+-----+ | ---
67 --------› 11:7| 5 | 9 | 14 (20) --------› ¤ | |
| +-----+-----+-----+ | |
| 78 ‹----- 12:8| 9 | 60 | 40 | 109 (26) «------------ | 11¨
| | +-----+-----+-----+ | | |
| | 86‹--- 13:9| 9 | 60 | 69 (27) «-- 2×Δ9 (2×MEC30) | {2®} | |
| | | +-----+-----+-----+ | | ---
| | ---› 14:10| 9 | 60 | 40 | 109 (28) ------------- | |
| | +-----+-----+-----+ | |
| ---› 15,18:11| 1 | 30 | 40 | 71 (29,30,31,32) ---------- 13¨
329 | +-----+-----+-----+ |
| ‹--------- 19:12| 10 | 60 | {70} (36) ‹--------------------- Φ |
-------------------+-----+-----+ ---
786 ‹------- 20:13| 90 | 90 (38) ‹-------------- ¤ |
| +-----+-----+ |
| 618 ‹- 21,22:14| 8 | 40 | 48 (40,41) ‹---------------------- ✔️ 17¨
| | +-----+-----+-----+-----+-----+ | |
| | 594 ‹- 23:15| 8 | 40 | 70 | 60 | 100 | 278 (42) «-- |{6'®} |
| | | +-----+-----+-----+-----+-----+ | | ---
--|--|-»24,27:16| 8 | 40 | 48 (43,44,45,46) ------------|---- ✔️ |
| | +-----+-----+ | |
--|---› 28:17| 100 | {100} (50) ------------------------» 19¨
168 | +-----+ |
| 102 -› 29:18| 50 | 50(68) --> 3×∆9-∆9=Δ18 goes to unknown |
----------------------+-----+ ---
Higgs Mechanism
109 + 30 + 30 = 139 + 30 = 169
In a quantum system, a physical state is described by a state vector:
- A pair of distinct state vectors are physically equivalent if they differ only by an overall phase factor, ignoring other interactions.
- A pair of indistinguishable particles such as this have only one state.
- This means that if the positions of the particles are exchanged (i.e., they undergo a permutation), this does not identify a new physical state, but rather one matching the original physical state.
In fact, one cannot tell which particle is in which position. (Wikipedia)
The Prime Recycling ζ(s):
(2,3), (29,89), (36,68), (72,42), (100,50), (2,3), (29,89), ...**infinity**
----------------------+-----+-----+-----+ ---
7 --------- 1,2:1| 1 | 30 | 40 | 71 (2,3) ‹-------------@---- |
| +-----+-----+-----+-----+ | |
| 8 ‹------ 3:2| 1 | 30 | 40 | 90 | 161 (7) ‹--- | 5¨
| | +-----+-----+-----+-----+ | | |
| | 6 ‹-- 4,6:3| 1 | 30 | 200 | 231 (10,11,12) ‹--|--- | |
| | | +-----+-----+-----+-----+ | | | ---
--|--|-----» 7:4| 1 | 30 | 40 | 200 | 271 (13) --› | {5®} | |
| | +-----+-----+-----+-----+ | | |
--|---› 8,9:5| 1 | 30 | 200 | 231 (14,15) ---------› | 7¨
289 | +-----+-----+-----+-----+-----+ | |
| ----› 10:6| 20 | 5 | 10 | 70 | 90 | 195 (19) --› Φ | {6®} |
--------------------+-----+-----+-----+-----+-----+ | ---
67 --------› 11:7| 5 | 9 | 14 (20) --------› ¤ | |
| +-----+-----+-----+ | |
| 78 ‹----- 12:8| 9 | 60 | 40 | 109 (26) «------------ | 11¨
| | +-----+-----+-----+ | | |
| | 86‹--- 13:9| 9 | 60 | 69 (27) «-- 2×Δ9 (2×MEC30) | {2®} | ✔️ |
| | | +-----+-----+-----+ | | ---
| | ---› 14:10| 9 | 60 | 40 | 109 (28) ------------- | |
| | +-----+-----+-----+ | |
| ---› 15,18:11| 1 | 30 | 40 | 71 (29,30,31,32) ---------- 13¨
329 | +-----+-----+-----+ |
| ‹--------- 19:12| 10 | 60 | {70} (36) ‹--------------------- Φ |
-------------------+-----+-----+ ---
786 ‹------- 20:13| 90 | 90 (38) ‹-------------- ¤ |
| +-----+-----+ |
| 618 ‹- 21,22:14| 8 | 40 | 48 (40,41) ‹---------------------- 17¨
| | +-----+-----+-----+-----+-----+ | |
| | 594 ‹- 23:15| 8 | 40 | 70 | 60 | 100 | 278 (42) «-- |{6'®} |
| | | +-----+-----+-----+-----+-----+ | | ---
--|--|-»24,27:16| 8 | 40 | 48 (43,44,45,46) ------------|---- |
| | +-----+-----+ | |
--|---› 28:17| 100 | {100} (50) ------------------------» 19¨
168 | +-----+ |
| 102 -› 29:18| 50 | 50(68) --> 3×∆9-∆9=Δ18 goes to unknown ✔️ |
----------------------+-----+ ---
Sun vs Moon
Thus a characteristic constant of this system depending on uniformperiods of the month and the year.
Since the presence of the sun changes the geometrical properties of space and time , we must screen out its gravitational effect on the earth moon system according to the validity condition of the second postulate of special relativity, i.e. we must only consider the lunar geocentric motion without the heliocentric motion of the earth-moon system. Thus a velocity component VO=V cosO representing the net orbital velocity of the moon as shown in fig. (1) is introduced for calculating the net length L of the lunar orbit assuming a stationary earth. (Determination Of The Greatest Speed C)
E = mc²
m = E/c²
c = 1 light-second
= 1000 years x L / t
= 12,000 months x 2152612.336257 km / 86164.0906 sec
= 299,792.4998 km / sec
Note:
1 year = 12 months
1000 years = 12,000 months
Te = earth revolution = 365,25636 days
R = radius of moon rotation to earth = 384,264 km
V = moon rotation speed = 2πR/Tm = 3682,07 km/hours
Ve = excact speed = V cos (360° x Tm/Te) = V cos 26,92848°
Tm = moon revolution (sidereal) = 27,321661 days = 655,719816 hours
t = earth rotation (sinodik) = 24 hours = 24 x 3600 sec = 86164.0906 sec
L = Ve x Tm = 3682,07 km/hours x cos 26,92848° x 655,71986 = 2152612.336257 km
Conclusion:
π(π(π(π(π(32(109²-89²)))))) Universe vs Unknown vs Unknowns (mass of matter)
👇
π(π(π(π(32(109²-89²))))) Galaxies vs Universe vs Unknown (gap in 2nd-level)
👇
π(π(π(32(109²-89²)))) Sun vs Galaxies vs Universe (2nd gap in 1st-level)
👇
π(π(32(109²-89²))) Moon vs Sun vs Galaxies (1st-gap via dark matter)
👇
|--👇---------------------------- 2x96 ---------------------|
|--👇----------- 7¤ ---------------|---------- 5¤ ----------|
|- π(32(109²-89²))=109² -|-- {36} -|-------- {103} ---------|
+----+----+----+----+----+----+----+----+----+----+----+----+
| 5 | 7 | 11 |{13}| 17 | 19 | 17 |{12}| 11 | 19 | 18 |{43}|
+----+----+----+----+----+----+----+----+----+----+----+----+
|--------- {53} ---------|---- {48} ----|---- {48} ----|109²-89² 👉
|---------- 5¤ ----------|------------ {96} -----------|-1¤-|
|-------- Bosons --------|---------- Fermions ---------|-- Graviton
|-- Sun Orbit (7 days) --|--- Moon Orbit (12 months) --| (11 Galaxies) ✔️
|------------ Part of 1 Galaxy (Milky Way) ------------| Non Milky Way
The number of primes less than or equal to a thousand π(1000) = 168 equals the number of hours in a week 24 × 7 = 168. The tessellating field of equilateral triangles fills with numbers, with spin orientation flipping with each prime number encountered, creating three (3) minor hexagons.
∆28 - ∆27 = 1000 - 900 + π(27/9) = 100 + 2 = 102 (Recycled to original state)
$True Prime Pairs:
(5,7),(11,13),(17,19)
|------------ 7'----------------|--------------------------- 12' ----------------------------|
| 3' | 4' | 6' | 6' |
+---+----+----+---+----+----+---+---+----+-----+----+----+----+----+----+-----+----+----+----+
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
+---+----+----+---+----+----+---+---+----+-----+----+----+----+----+----+-----+----+----+----+
| 2 | 60 | 40 | 1 | 30 | 30 | 5 | 1 | 30 | 200 | 8 | 40 | 50 | 1 | 30 | 200 | 8 | 10 | 40 |
+---+----+----+---+----+----+---+---+----+-----+----+----+----+----+----+-----+----+----+----+
| Z | W± | γ | A H+ H- hH | u c t g γ eμτ | d s b g ν¤ γ |
|---- 102 ---|----- 66 ------|-------- 329 = 7 x 47 -------|- 289 = (8+9)² = 2 & (2³+9²) -|
|--2x3x(8+9)--|--- 2x3x(2+9) ---|---- (1+2) & (2x9)+(2+9) ----|------ 2 & (8x9)+(8+9) -------|
|-------- 168 = π(1000) --------|------ 1229 = π(10000) ------|------ π(89²) = 1000 ---------|
|-------- 168 = π(618xΦ) -------|----- 618 = 1000/Φ = 1000x1000/1618 = 10^6/(2x8)&(2x9) -----|
In particle physics, a lepton is an elementary particle of half-integer spin (spin 1⁄2) that does not undergo strong interactions.[1]
- Two main classes of leptons exist: charged leptons (also known as the electron-like leptons or muons), and neutral leptons (better known as neutrinos).
- Charged leptons can combine with other particles to form various composite particles such as atoms and positronium, while neutrinos rarely interact with anything, and are consequently rarely observed.
- The best known of all leptons is the electron.
There are six types of leptons, known as flavours, grouped in three generations.[2]
- The first-generation leptons, also called electronic leptons, comprise the electron (e−) and the electron neutrino (νe); the second are the muonic leptons, comprising the muon (μ−) and the muon neutrino (νμ); and the third are the tauonic leptons, comprising the tau (τ−) and the tau neutrino (ντ).
- Electrons have the least mass of all the charged leptons. The heavier muons and taus will rapidly change into electrons and neutrinos through a process of particle decay: the transformation from a higher mass state to a lower mass state.
- Thus electrons are stable and the most common charged lepton in the universe, whereas muons and taus can only be produced in high energy collisions (such as those involving cosmic rays and those carried out in particle accelerators).
- Leptons have various intrinsic properties, including electric charge, spin, mass.
- Unlike quarks, however, leptons are not subject to the strong interaction, but they are subject to the other three fundamental interactions: gravitation, the weak interaction, and to electromagnetism, of which the latter is proportional to charge, and is thus zero for the electrically neutral neutrinos.
For every lepton flavor, there is a corresponding type of antiparticle, known as an antilepton, that differs from the lepton only in that some of its properties have equal magnitude but opposite sign. According to certain theories, neutrinos may be their own antiparticle. It is not currently known whether this is the case. (Wikipedia)
It is stated that if vector of the composite system is mathematically equivalent then the entangled states of the two particles are different (otherwise the antisymmetric state vector would vanish).
The aim of this paper is to offer a conceptual analysis of Weinberg’s proof of the spin-statistics theorem by comparing it with Pauli’s original proof and with the subsequent textbook tradition, which typically resorts to the dichotomy positive energy for half-integral spin particles/micro causality for integral-spin particles.
- In contrast to this tradition, Weinberg’s proof does not directly invoke the positivity of the energy, but derives the theorem from the single relativistic requirement of micro causality. This seemingly innocuous difference marks an important change in the conceptual basis of quantum physics.
- Its historical, theoretical, and conceptual roots are here reconstructed. The link between Weinberg’s proof and Pauli’s original is highlighted: Weinberg’s proof turns out to do justice to Pauli’s anti-Dirac lines of thought.
The work of Furry and Oppenheimer is also surveyed as a “third way” between the textbook tradition established by Pauli and Weinberg’s approach - pdf
This is nothing but Pauli's Exclusion Principle forbidding the possibility of any two indistinguishable particles being in the same dynamic state (Pauli, 1925).
Irrational Partitions
By this exponentiation zones we will get multiple layers of primes density. So we need to get in to the patterns of the above hexagonal forms through deep learning.
SU(5) fermions of standard model in 5+10 representations. The sterile neutrino singlet’s 1 representation is omitted. Neutral bosons are omitted, but would occupy diagonal entries in complex superpositions. X and Y bosons as shown are the opposite of the conventional definition
[(6 + 6) x 6] + [6 + (6 x 6)] = 72 + 42 = 71 + 42 + 1 = 114 objects
layer | node | sub | i | f
------+------+-----+----------
| | | 1 | ----------------------- 71 = 72-1
| | 1 +-----+ |
| 1 | | 2 | (5) |
| |-----+-----+ |
| | | 3 | --------- |
1 +------+ 2 +-----+---- | |
| | | 4 | 5x --- |
| +-----+-----+ | | |
| 2 | | 5 | (7) ----- | |
| | 3 +-----+ | |
289+11=300 | | 6 | | |
------+------+-----+-----+----- 72 x 6 7x --- 11x = 77 (rational)
| | | 7 | | |
| | 4 +-----+ | |
| 3 | | 8 | (11) --- | |
| +-----+-----+ | | |
| | | 9 | 2x --- |
2 +------| 5 +-----+----- | |
| | | 10 | --------- |
| |-----+-----+ |
| 4 | | 11 | (13) ------------------ 71 = 72-1
| | 6 +-----+
329+71=400 | | 12 |------------------------ 70 = 72-2
------+------+-----+-----+
| | | 13 |
| | 7 +-----+
| 5 | | 14 | (17) ◄---------------------------
| |-----+-----+
| | | 15 | ◄-- 42 x 6 partitions of 13 (irrational)
3 +------+ 8 +-----+-----
| | | 16 | ◄---------------------------
| |-----+-----+
| 6 | | 17 | (19)
| | 9 +-----+
168+32=200 | | | 18 |------------------------ 68 = 72-4
------|------|--|--+-----+
900 -----
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum mechanics. It is a key result in quantum-mechanical system, and its discovery was a significant landmark in the development of the subject.
Complex plot of a wave function that satisfies the nonrelativistic Schrödinger equation with V = 0. In other words, this corresponds to a particle traveling freely through empty space (Wikipedia).
The Prime Recycling ζ(s):
(2,3), (29,89), (36,68), (72,42), (100,50), (2,3), (29,89), ...**infinity**
----------------------+-----+-----+-----+ ---
7 --------- 1,2:1| 1 | 30 | 40 | 71 (2,3) ‹-------------@---- ✔️ |
| +-----+-----+-----+-----+ | |
| 8 ‹------ 3:2| 1 | 30 | 40 | 90 | 161 (7) ‹--- | 5¨
| | +-----+-----+-----+-----+ | | |
| | 6 ‹-- 4,6:3| 1 | 30 | 200 | 231 (10,11,12) ‹--|--- | |
| | | +-----+-----+-----+-----+ | | | ---
--|--|-----» 7:4| 1 | 30 | 40 | 200 | 271 (13) --› | {5®} | |
| | +-----+-----+-----+-----+ | | |
--|---› 8,9:5| 1 | 30 | 200 | 231 (14,15) ---------› | 7¨
289 | +-----+-----+-----+-----+-----+ | |
| ----› 10:6| 20 | 5 | 10 | 70 | 90 | 195 (19) --› Φ | {6®} |
--------------------+-----+-----+-----+-----+-----+ | ---
67 --------› 11:7| 5 | 9 | 14 (20) --------› ¤ | |
| +-----+-----+-----+ | |
| 78 ‹----- 12:8| 9 | 60 | 40 | 109 (26) «------------ | 11¨
| | +-----+-----+-----+ | | |
| | 86‹--- 13:9| 9 | 60 | 69 (27) «-- 2×Δ9 (2×MEC30) | {2®} | |
| | | +-----+-----+-----+ | | ---
| | ---› 14:10| 9 | 60 | 40 | 109 (28) ------------- | |
| | +-----+-----+-----+ | |
| ---› 15,18:11| 1 | 30 | 40 | 71 (29,30,31,32) ------------ ✔️ 13¨
329 | +-----+-----+-----+ |
| ‹--------- 19:12| 10 | 60 | {70} (36) ‹--------------------- Φ |
-------------------+-----+-----+ ---
786 ‹------- 20:13| 90 | 90 (38) ‹-------------- ¤ |
| +-----+-----+ |
| 618 ‹- 21,22:14| 8 | 40 | 48 (40,41) ‹---------------------- 17¨
| | +-----+-----+-----+-----+-----+ | |
| | 594 ‹- 23:15| 8 | 40 | 70 | 60 | 100 | 278 (42) «-- |{6'®} |
| | | +-----+-----+-----+-----+-----+ | | ---
--|--|-»24,27:16| 8 | 40 | 48 (43,44,45,46) ------------|---- |
| | +-----+-----+ | |
--|---› 28:17| 100 | {100} (50) ------------------------» 19¨
168 | +-----+ |
| 102 -› 29:18| 50 | 50(68) --> 3×∆9-∆9=Δ18 goes to unknown |
----------------------+-----+ ---
A set of conceptual problems has to be solved, including a superposition principle which requires a linear vector field and quantisation of space-time itself.
The approach taken is to think of the solutions of an equation as a geometric object. For example, an equation in two variables defines a curve in the plane. More generally, an equation, or system of equations, in two or more variables defines a curve, a surface or some other such object in n-dimensional space (Wikipedia).

Consider this could only be solved by prime theory. An experimental observation of the graviton, the gravitational force carrier, is extremely hard due to small coupling.
$True Prime Pairs:
(5,7), (11,13), (17,19)
| 168 | 618 |
-----+-----+-----+-----+-----+ ---
19¨ | 3¨ | 4¨ | 6¨ | 6¨ | 4¤ ✔️ ---> assigned to "id:30" 19¨
-----+-----+-----+-----+-----+ ---
17¨ | .. | .. | .. | .. | 4¤ -----> assigned to "id:31" |
+-----+-----+-----+-----+ |
{12¨}| .. | .. | 2¤ (M & F) -----> assigned to "id:32" |
+-----+-----+-----+ |
11¨ | .. | .. | .. | 3¤ ----> Np(33) assigned to "id:33" -----> 👉 77¨
-----+-----+-----+-----+-----+ |
19¨ | .. | .. | .. | .. | 4¤ -----> assigned to "id:34" |
+-----+-----+-----+-----+ |
{18¨}| .. | .. | .. | 3¤ -----> assigned to "id:35" |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
43¨ | .. | .. | .. | .. | .. | .. | .. | .. | .. | 9¤ (C1 & C2) 43¨
-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
139¨ | 1 2 3 | 4 5 6 | 7 8 9 |
Δ Δ Δ
This idea was taken as the earliest in 1960s Swinnerton-Dyer by using the University of Cambridge Computer Laboratory to get the number of points modulo p (denoted by Np) for a large number of primes p on elliptic curves whose rank was known.
In the early 1960s Peter Swinnerton-Dyer used the EDSAC computer to calculate the number of points modulo p (denoted by Np) for a large number of primes p on elliptic curves whose rank was known.
- Based on these numerical results, Birch & Swinnerton-Dyer (1965) conjectured that Np for a curve E with rank r obeys an asymptotic law.
- The conjecture predicts that the data should form a line of slope equal to the rank of the curve, which is 1 in this case drawn in red in red on the graph
The Birch and Swinnerton-Dyer conjecture, considered one of the top unsolved problems in mathematics as of 2022. (Wikipedia).